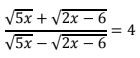Category: Maths

MATHEMATICS 

SECTION A

 

Q. 1 (a) If b is the mean proportion between a and c, show that: 

 

(b) Solve the equation 4×2 – 5x – 3 = 0 and give your answer correct to two decimal places. 

(c) AB and CD are two parallel chords of a circle such that AB = 24 cm and CD = 10 cm. If the radius of the circle is 13 cm, find the distance between the two chords. 

Solution :

(a) Here, b is the mean proportion between a and c.

∴ b² = ac

(b) Given equation is :

4x² – 5x – 3 =0

By using quadratic formula, we obtain

(c) Here, O is the centre of the given circle of radius 13 cm. AB and CD are two parallel chords, such that AB = 24 cm and CD = lo cm.

Join OA and OC.

Since ON⊥AB and 0M ⊥CD.

∴ M, O and N are collinear and M, N are mid-points of CD and AB.

Now, in rt. ∠ed ∆ANO, we have

ON² = 02 AN²

= 13²– 12²

= 169 – 144 = 25

ON= √25 = 5cm

Similarly, in it. ∠ed ∆CMO, we have

OM2 = OC² – CM²

= 13² – 5²

= 169 – 25 = 144

0M = √144= 12cm

Hence, distance between the two chords

NM = NO + OM

= 5 + 12

= 17 cm

Q. 2. (a) Evaluate without using trigonometric tables,  sin²28° + sin²62° + tan²38° – cot²52° + sec²30°

(b) If A =  and A² – 5B² = 5C. Find matrix C where C is a 2 by 2 matrix. 

(c) Jaya borrowed ₹ 50000 for 2 years. The rates of interest for two successive years are 12% and 15% respectively. She repays ₹ 33000 at the end of the first year. Find the amount she must pay at the end of the second year to clear her debt. 

Solution :

(b) Here, A =

Now, A2 = AA

B2 = BB

Again, 5C = A2 – 5B2

(c) Principal = ; 50000

Time =1 year

Rate = 12%

Q. 3. (a) The catalogue price of a computer set is 42000. The shopkeeper gives a discount of 10% on the listed price. He further gives an off-season discount of 5% on the discounted price. However, sales tax at 8% is charged on the remaining price after the two successive discounts. Find: 

(i) the amount of sales tax a customer has to pay.

(ii) the total price to be paid by the customer for the computer set.

(b) P(1, – 2) is a point on the line segment A(3, – 6) and B(x, y) such that AP : PB is equal to 2 : 3. Find the coordinates of B. 

(c) The marks of 10 students of a class in an examination arranged in ascending order is as follows : 

13, 35, 43, 46, x, x + 4, 55, 61, 71, 80

If the median marks is 48, find the value of x. Hence, find the mode of the given data

Solution :

Hence, amount of sales tax is ₹ 2872.80 and total price to be paid by the customer for the computer set is ₹ 38782.80.

(b) Here, AP : PB = 2 : 3, therefore, P divides AB in the ratio 2 : 3

Thus, coordinates of P are:

Also, coordinates of P are P(1, – 2)

Hence, coordinates of B are B ( – 2, 4).

(c) Here, number of students are 10 i.e., even number of observations.

Thus, the observations are 13, 35, 43, 46, 46, 50, 55, 61, 71, 80.

Hence, the mode of the given data is 46.

Q.4. (a) What must be subtracted from 16x³ – 8x² + 4x + 7 so that the resulting expression has 2x + 1 as a factor? 

(b) In the given figure ABCD is a rectangle. It consists of a circle and two semi-circles each of which are of radius 5 cm. Find the area of the shaded region. Give your answer correct to three significant figures.

(c) Solve the following inequation and represent the solution set on a number line. 

Solution:

(a) Let p(x) = 16x³ – 8x² + 4x + 7 and g(x) = 2x + I

Put 2x + 1 = 0 ⇒ x = – 1/2

Hence, 1 is subtracted from p(x), so that g(x) is a factor of p(x).

(b) Here, radius of a circle and two semi-circles = 5 cm

Length of the rectangle = 5 + 10 + 5 = 20 cm

Breadth of the rectangle = 10 cm

Now, area of the shaded part = Area of rectangle – 2 × Area of circle

(c) Given inequation is :

Solution set on number line

SECTION B 

Attempt any four Q. s from this Section

Q. 5. (a) Given matrix B = . Find the matrix X if, X=B2 – 4B. 

Hence, solve for a and b given

(b) How much should a man invest in 50 shares selling at 60 to obtain an income of 450, if the rate of dividend declared is 10%. Also, find his yield percent, to the nearest whole number. 

(c) Sixteen cards are labelled as a, b, c … m, n, o, p. They are put in a box and shuffled. A boy is asked to draw a card from the box. What is the probability that the card drawn is : 

(i) a vowel

(ii) a consonant

(iii) none of the letters of the word median? 

Solution :

Market value of a share = ₹ 60

Face value of a share = ₹ 50

Rate of dividend = 10%

Total income = ₹ 450

If income is 5, then investment = ₹ 60

If income is 1, then investment = 60/5 = ₹ 12

If income is 450, then investment = ₹ 12 × 450

= ₹ 5400

Thus, total investment is ₹ 5480

∴ Yield percent =( 450/5400) × 100 = 8.33

= 8 (to the nearest whole number)

(c) Total number of cards = 16

(i) Number of vowels = 4 (a, e, i, o)

Probability = 4/16= 1/4

(ii) Numberofeonsonant = 16 – 4 = 12

Probability = 12/16 = 3/4

(iii) Probability (none of the letters of the word median) = 10/16 = 5/8

 

Q.6.(a) Using a ruler and a corrpass construct a triangle ABC in which AB = 7 cm, ∠CAB = 600 and AC = 5 cm. Construct the locus of : 

(i) points equidistant from AB and AC.

(ii) points equidistant from BA and BC.

Hence, construct a circle touching the three sides of the triangle internally.

(b) A conical tent is to accommodate 77 persons. Each person must have 16 n? of air to breathe. Given the radius of the tent as 7 m, find the height of the tent and also its curved surface area. 

(c) If  (7m+2n)/(7m−2n) =  5/3 , use properties of proportion to find :

(i) m : n

(ii) (m²+n²)/(m²−n²)

Solution :

(a) Steps of Construction :

1. Draw a line segment AB = 7 cm.

2. At A construct an angle of 600 such that AC = 5 cm.

3. Join BC to get ∆ABC.

4. Draw angle bisector of ∠BAC, which is the required locus of the points equidistant from AB and AC.

5. Draw angle bisector of ∠ABC, which is the required locus of the points equidistant from BA and BC.

6. Let the two angle bisectors intersect each other in I.

7. Through I, draw ID⊥AB. With I as centre and radius = ID draw a circle which touches all the sides of the ∆ABC internally.

Total number of persons accommodated = 77

Volume of air required for each person = 16 m³

Volume of the conical tent = 77 × 16

= 1232 m³

Radius of the tent = 7 m

Let h be the height of the conical tent

Using componendo and dividendo, we have

[Using componendo and dividendo]

 

Q. 7. (a) A page from a savings bank account passbook is given below: 

(i) Calculate the interest for the 6 months from January to June 2016, at 6% per annum.

(ii) If the account is closed on 1st July 2016, find the amount received by the account holder.

(b) Use a graph paper for this Q.  (Take 2 cm =1 unit on both x and y axis) 

(i) Plot the following points:

A(0, 4), B(2, 3), C(1, 1) and D(2, 0).

(ii) Reflect points B, C, D on the y-axis and write down their coordinates. Name the images as B’, C’, D’ respectively.

(iii) Join the points A, B, C, D, D’, C’,B’ and A in order, so as to form a closed figure. Write down the equation of the line of symmetry of the figure formed.

Solution :

(a) Minimum balance for the month Jan., 2016 = ₹ 5600

Minimum balance for the month Feb., 2016 = ₹ 4100

Minimum balance for the month Mar., 2016 = ₹ 4100

Minimum balance for the month Apr., 2016 = ₹ 2000

Minimum balance for the month May, 2016 = ₹  8500

Minimum balance for the month June, 2016 = ₹ 10000

Total = ₹ 34300

Principal = ₹ 34300

Rate = 6% p.a.

Time = 1/12 year

(b) (E) On graph ,

(ii) B’(- 2, 3), C’(- 1, 1), D’(- 2, 0)

(iii) Equation of the line of symmetry is x = O

Q.8. (a) Calculate the mean of the following distribution using step deviation method. 

(b) In the given figure PQ is a tangent to the circle at A. AB and AD are bisectors of ∠CAQ and ∠PAC. If ∠BAQ = 30° prove that :

(i) BD is a diameter of the circle.

(ii) ABC is an isosceles triangle.

(C) The printed price of an air conditioner is ₹ 45000/-. The wholesaler allows a discount of 10% to the shopkeeper. The shopkeeper sells the article to the customer at a discount of 5% of the marked price. Sales tax (under VAT) is charged at the rate of 12% at every stage. Find :

(i) VAT paid by the shopkeeper to the government.

(ii) The total amount paid by the customer inclusive of tax. 

Solution :

Let assumed mean (a) = 35

(b) Here PQ, is a tangent of the circle at A .

∠BAQ = 30°. Since AB is

angle bisector of ∠CAQ.

∴ ∠CAB = ∠BAQ = 30°

Again, ∠PAC = 180° – ∠CAQ

= 180°- 30°- 30°

= 120°

Also, AD is angle bisector of ∠PAC

∴ ∠PAD = ∠CAD = 60°

Since angles in the corresponding alternate segment are equal

∴ ∠ADB =∠BAQ = 30° and ∠DBA = ∠PAD = 60°

Also, angles in same segment are equal

∴ ∠DCA = ∠DBA = 60°

and ∠ACB = ∠ADB = 30°

Now, ∠DCB = ∠DCA + ∠ACB = 60° + 30° = 90°

We know that angle in a semi-circle is right angle.

Thus, BD is a diameter of the circle.

In ∆ACB, ∠ACB = ∠CAB = 30°

Hence, ∆ABC is an isosceles triangle.

List price of air conditioner = 45000

Discount = 10%

Thus, VAT paid by the shopkeeper to the government = ₹ (5130 – 4860) = ₹ 270

Total amount paid by the customer = ₹ (42750 + 5130) = ₹ 47880

 

Q. 9. (a) In the figure given, O is the centre of the circle. LDAE = 700.

Find giving suitable reasons, the measure of: 

(i) ∠BCD

(ii) ∠BOD

(iii) ∠OBD

(b) A(-1, 3), B(4, 2) and C(3, -2) are the vertices of a triangle. 

(i) Find the coordinates of the centroid G of the triangle.

(ii) Find the equation of the line through G and parallel to AC.

(c) Prove that: 

Solution :

(a) Here, ∠DAE = 70°

∴ ∠BAD = 180° ∠DAE

[a linear pair]

= 180° – 70° = 110°

ABCD is a cyclic quadrilateral

∴ ∠BCD + ∠BAD = 180°

∠BCD + 110° = 180°

⇒ ∠BCD = 180° – 110°

= 70°

Since angle subtended by an arc at the centre of a circle is twice the angle subtended at the remaining part of the circle.

∴ ∠BOD = 2∠BCD = 2 × 70° = 140°

In ∆OBD, OB = OD = radii of same circle.

∴ ∠OBD =∠ODB

Thus, ∠OBD = 1/2 (180° – ∠BOD) = 1/2 (180° – 140°) = 1/2 × 40° = 20°

(b) A(-1, 3), B(4, 2) and C(3, -2) are the vertices of ∆ABC.

∴ Coordinates of the centroid G of the ∆ABC are :

G(2, 1)

Here, line ‘l’ is drawn through G(2, 1) and parallel to the line AC.

∴ Slope of the line l = Slope of the line AC

(−2−3)/(3+1) = −5/4

y – 1 = (−5/4) (x – 2)

4y – 4 = – 5x + 10

5x + 4y = 14

Q. 10. (a) The sum of the ages of Vivek and his younger brother Amit is 47 years. The product of their ages in years is 550. Find their ages. 

(b) The daily wages of 80 workers in a project are given below

Use a graph paper to draw an ogive for the above distribution. (Use a scale of 2 cm = ₹ 50 on x-axis and 2 cm = 10 workers on y-axis. Use your ogive to estimate:

(i) the median wage of the workers.

(ii) the lower quartile wage of workers.

(iii) the number of workers who earn more than ₹ 625 daily.

Solution:

(a) Let Vivek’s age be x years

∴ Amit’s age = 47 – x

Also, product of their ages = 550

∴ x(47 – x) = 550

47x – x² = 550

⇒ x² – 47x + 550 =0

⇒ x² – 25x – 22x + 550 = 0

⇒ x(x – 25) – 22(x – 25) = 0

⇒ (x – 25)(x – 22)= 0

⇒ x = 25

or x = 22

Since Vivek is elder brother of Amit.

Hence, age of Vivek is 25 years and age of Amit is 22 years.

(b) The cumulative frequency distribution for the given data is :

Plot the points (450, 2), (500, 8), (550, 20), (600, 38), (650, 62), (700, 75), (750, 80).

Join them free hand to get the required ogive.

Now, from the graph, we obtain:

(i) median wage of the workers = ₹ 605

(ii) lower quartile wage of workers = ₹ 550

(iii) Number of workers who earn more than ₹ 625 daily = 80 – 50 = 30.

Q. 11. (a) The angles of depression of two ships A and B as observed from the top of a light house 60 m high are 60° and 45° respectively. If the two ships are on the opposite sides of the light house, find the distance between the two ships. Give your answer correct to the nearest whole number. 

(b) PQR is a triangle. S is a point on the side QR of ∆PQR such that

∠PSR = ∠QPR.

Given QP = 8 cm, PR = 6 cm and SR = 3 cm. 

(i) Prove ∆PQR ~ ∆SPR

(ii) Find the length of QR and PS

(iii) (area of ΔPQR)/( area of ΔSPR)

(c) Mr. Richard has a recurring deposit account in a bank for 3 years at 7.5% p.a. simple interest. If he gets ₹ 8325 as interest at the time of maturity, find : 

(i) The monthly deposit

(ii) The maturity value.

Solution:

(a) Let PQ be the light house of height 60m, A and B are the two ships on the opposite sides of the light house, such that:

∠PAQ = 60°, ∠PBQ= 45°

In rt ∠ed ∆PQB, we have

PQ/QB

 = tan 45° = 1

⇒ PQ =QB = 60 m

In rt ∠ed ∆PQA, we have

Now, AB = AQ + QB = 60 + 34.6 = 94.6m

Hence, the distance between the two ships is 95 m (nearest to whole number).

(b) Given : QP = 8 cm, PR = 6 cm and SR = 3 cm

In ∆PQR and ∆SPR

∠QPR = ∠PSR (given)

∠QRP = ∠SRP (common)

∴ ∆PQR ~ ∆SPR (by AA similarity rule)

Since ∆PQR ~ ∆SPR

(c) Let the monthly deposit be ₹ x

Time = 3 years or 36 months, R = 7.5%, Interest = ₹ 8325.

Thus, the monthly deposit is ₹ 2000

The maturity value = ₹ 36 × 2000 + ₹ 8325

= ₹ 72000 + ₹ 8325 = ₹ 80325

 

MATHEMATICS 

SECTION A

Q.  1 (a) Find the value of ‘x’ and ‘y’ if: 

(b) Sonia had a recurring deposit account in a bank and deposited `600 per month for 2½ years. If the rate of interest was 10% p.a., find the maturity value of this account. 

(c) Cards bearing numbers 2, 4, 6, 8, 10, 12, 14, 16, 18 and 20 are kept in a bag. A card is drawn at random from the bag. Find the probability of getting a card which is: 

    (i) a prime number. 

    (ii) a number divisible by 4. 

   (iii) a number that is a multiple of 6. 

   (iv) an odd number. 

Answer:

⇒ 2 JC + 6 = 10 ⇒ 2x = 4 ⇒ x = 2

And 2y – 5 = 15 ⇒ 2y = 20 ⇒ y = 10

Hence, the values of x and y are x = 2 and y = 10

(b) Here, amount deposited per month = ₹ 600

       Number of months = 2 x 12 + 6 = 30  [∵ v T = 2.5years]

        Rate of interest = 10% p.a.

Hence, the amount received by Sonia on maturity is ₹ 20325.

(c) Total number of cards in the bag = 10

(i) Total prime numbers = 1 i.e., 2

∴ Required Probability = 110

(ii) Total numbers divisible by 4 = 5 (i.e., 4, 8, 12, 16, 20]

Required Probability = 510=12

(iii) Total numbers divisible by 6 or multiple of 6 = 3 [i.e., 6, 12, 18]

∴ Required Probability = 310

(iv) Total odd number = 0

∴ Required Probability =010 = 0.

 

Q.  2 (a) The circumference of the base of a cylindrical vessel is 132 cm and its height is 25 cm. Find the  

    (i) radius of the cylinder 

    (ii) volume of cylinder. (use π =227) 

(b) If (k –3), (2k + 1) and (4k + 3) are three consecutive terms of an A.P., find the  value of k. 

(c) PQRS is a cyclic quadrilateral. Given ∠QPS = 73^o, ∠PQS = 55^oand ∠PSR = 82^o,calculate: 

(i) ∠QRS 

(ii) ∠RQS 

(iii) ∠PRQ 

Answer :

(a) Let r be the radius of the base of cylindrical vessel and ft = 25 cm be its height.

Now, circumference of the base = 132 cm

2πr = 132

Hence, the radius of the cylinder is 21 cm and volume of the cylinder is 34650 cm³

(b) Here, ft – 3, 2k + 1 and 4k + 3 are three consecutive terms of an A.P.

∴ 2k + 1 – (k – 3) = 4k + 3 – (2k + 1)

⇒ 2k + 1 – k + 3 = 4k + 3 – 2k – 1

⇒ k + 4 = 2k + 2

⇒ 2k – k =4 – 2

⇒ k = 2

Hence, the value of ft is 2.

(c)(i) Since PQRS is a cyclic quadrilateral

∠QPS + ∠QRS – 180°

⇒ 73° + ∠QRS = 180°

⇒ ∠QRS = 180° – 73°

∠QRS = 107°

(ii) Again, ∠PQR + ∠PSR = 180°

∠PQS + ∠RQS + ∠PSR = 180°

55° – ∠RQS + 82° = 180°

∠RQS = 180° – 82° – 55° = 43°

(iii) In ∆PQS, by using angles sum property of a ∆.

∠PSQ + ∠SQP + ∠QPS = 180°

∠PSQ + 55° + 73° = 180°

∠PSQ = 180° – 55° – 73°

∠PSQ = 52°

Now, ∠PRQ = ∠PSQ = 52° [∠s of the same segment]

Hence, ∠QRS = 107°, ∠RQS = 43° and  ∠PRQ = 52°

Q.  3 (a) If (x+ 2) and (x + 3) are factors of x³ + ax + b, find the values of ‘a’ and ‘b’. 

(b) Prove that sec²θ+cosec²θ  = tanθ + cot θ

(c) Using a graph paper draw a histogram for the given distribution showing the number of runs scored by 50 batsmen. Estimate the mode of the data: 

Runs  scored	3000- 4000	4000- 5000	5000- 6000	6000- 7000	7000- 8000	8000- 9000	9000- 10000
No. of  batsmen	4	18	9	6	7	2	4

Answer :

(a) Given that (x + 2) and (x + 3) are factors of p(x) = x³ + ax + b.

∴ p(- 2) = (- 2)³ + o(- 2) + b = 0

⇒ – 8 – 2a + b = 0 => – 2a + b = 8 …….(i)

And p(- 3) = (- 3)³ + a(- 3) + b = 0

⇒ – 27 – 3a + b = 0 => – 3a + b = 27 ……..(ii)

Subtracting (i) from (ii), we obtain

(- 3a 4 – b) – (- 2a + b) = 27 – 8

– 3a + b + 2a – b = 19

-a = 19

⇒ a = 19

From (i), we obtain

– 2(19) + b = 8

– 38 + b = 8

⇒ b = 8 + 38

⇒ b = 46

Hence, the values of a and b are a = 19 and b = 46.

Q.  4 (a) Solve the following inequation, write down the solution set and represent it on the real number line: 

    −2 + 10x ≤ 13x + 10 < 24 + 10x, x ∈ Z

(b) If the straight lines 3x − 5y = 7 and 4x + ay + 9 = 0 are perpendicular to one another, find the value of a. 

(c) Solve x² + 7x = 7 and give your answer correct to two decimal places. 

Answer.

(a)

 Given that :

Thus, the required solution set is :

Using number line, we have

(b)Given lines are

3x – 5y = 1 ……….(i) and 4x + ay + 9 = 0  …………(ii)

Slope of line (i) (m1) =  −(3-5)=35

Slope of line (ii) (m2) = −(4a)

Also, given that two lines are perpendicular to one and another

∴ (m1) (m2) = – 1

⇒

Hence, the value of a = 125 .

(c) Here, x² + 7x = 7

⇒ x² + 7x – 7 = 0

SECTION B 

Q.  5 (a) The 4^th term of a G.P. is 16 and the 7^th term is 128. Find the first term and common ratio of the series. 

(b) A man invests `22,500 in `50 shares available at 10% discount. If the dividend paid by the company is 12%, calculate: 

    (i) The number of shares purchased 

    (ii) The annual dividend received. 

    (iii) The rate of return he gets on his investment. Give your answer correct to the nearest whole number. 

(c) Use graph paper for this Q.  (Take 2cm = 1unit along both x and y axis).  

     ABCD is a quadrilateral whose vertices are A(2,2), B(2,–2), C(0,–1) and D(0,1). 

    (i) Reflect quadrilateral ABCD on the y-axis and name it as A’B’CD.  

    (ii) Write down the coordinates of A’ and B’. 

   (iii) Name two points which are invariant under the above reflection. 

   (iv) Name the polygon A’B’CD. 

Answer.

(a) Let a and r be the first term and common ratio of given G.P.

∴ a⁴ = 16

⇒ ar³ = 16

and a⁷= 128

⇒ a⁶ = 128

Dividing (ii) and (i), we obtain

a³ = 3

a³= 23

a = 2

⇒

From (i), we have

2(r³) = 16

r³ = 8

r³ = 23

⇒ r = 2

Hence, the first term and common ratio of the given series is 2 and 2.

(b) Total investment = ₹ 22,500

Face value of a share = ₹ 50

Market value of a share = ₹ (50 – 10% of 50) = ₹ (50 – 5) = ₹ 45

∴ No. of shares purchased = 2250045= 500

Annual dividend per share = 12 % of 50

Total annual dividend = ₹ 6 × 500 = ₹ 3000

Rate of return =

= 13.3 %

= 13% (Nearest whole number)

Hence, number of shares purchased are 500, total annual dividend is ₹ 3000 and rate of return on investment is nearly 13 % p. a.

(c) Scale used is : 2 cm = 1 unit along both x and y axis.

(i) Here, vertices of the quadrilateral ABCD are A(2, 2), B(2, -2), C(0, -1) and D(0, 1)

(iii) Two points which are invariant are C and D.

(iv) A’B’CD is a trapezium.

Q.  6 (a) Using properties of proportion, solve for x. Given that x is positive: 

(c) Prove that (1 + cotθ−cosecθ)(1 + tanθ+ secθ)= 2

Answer.

(a)

By componendo and Dividendo, we have

Squaring both sides, we have

Hence the value of x is 58

(b) Given that

(c) L.H.S. = (1 +cot θ – cosec θ) (1 + tan θ + sec θ)

Q.  7 (a) Find the value of k for which the following equation has equal roots. 

                         x² + 4kx + (k² − k + 2) = 0 

(b) On a map drawn to a scale of 1 : 50,000, a rectangular plot of land ABCD has the following dimensions. AB = 6cm; BC = 8cm and all angles are right angles. Find: 

   (i) the actual length of the diagonal distance AC of the plot in km. 

  (ii) the actual area of the plot in sq km. 

(c) A(2, 5), B(–1, 2) and C(5, 8) are the vertices of a triangle ABC, ‘M’ is a point on AB such that AM : MB = 1 : 2. Find the co-ordinates of ‘M’. Hence find the  equation of the line passing through the points C and M. 

Answer.

(a) Given quadratic equation is :

x² + 4kx + (k² – k + 2) = 0

For equal roots, we have

b²– 4 ac = 0

⇒ (4k)² – 4(1) (k²-k + 2) = 0

⇒ 16k² – 4k² + 4k – 8 = 0

⇒ 12k²+ 4k – 8 = 0

or 3k² + k – 2 = 0

⇒ 3k² + 3k – 2k -2 = 0

⇒ 3k(k + 1) – 2(k + 1) = 0

⇒ (k + 1)(3k – 2) = 0

⇒ k + 1=0 or 3k – 2 = 0

k = – 1 or k = 23

(b) Scale used on the map is 1 : 50,000

Dimensions of a rectangular plot ABCD are AB = 6 cm, BC = 8 cm Since each angle is right angle

∴ By using Pythagoras theorem, we have

(i) Actual length of the diagonal AC = 10 × 50000 cm

= 500000100000km

= 5 km

(ii) Area of the rectangular field ABCD on map

= 6 × 8 = 48 cm2

Actual area of the field = 48 × 500000 × 500000

= 12(10)10 sq. cm.

= 12 sq. km.

(c) Coordinates of the vertices of a ∆ ABC are A(2, 5), B(- 1, 2) and C (5, 8). Since M is a point on AB such that AM : MB = 1 : 2

Coordinates M are

Now, equation of the line CM is given as :

Q.  8 (a) ₹ 7500 were divided equally among a certain number of children. Had there been 20 less children, each would have received ₹100 more. Find the original number of  children. 

(b) If the mean of the following distribution is 24, find the value of ‘a’. 

Marks	0 – 10	10 – 20	20 – 30	30 – 40	40 – 50
Number of  students	7	a	8	10	5

(c) Using ruler and compass only, construct a ∆ABC such that BC = 5 cm and AB = 6.5

      cm and ∠ABC = 120^° 

   (i) Construct a circum-circle of ∆ABC 

  (ii) Construct a cyclic quadrilateral ABCD, such that D is equidistant from AB and  BC. 

Answer.

(a) Total amount = ₹ 7500

Let the number of children be x

∴ Share of each child = ₹7500x 

According to the statement

(x – 20) (7500 + 100x) = 7500 x

7500x + 100x²– 150000 – 2000x – 7500x = 0

100x² – 200x – 150000 = 0

x² – 20x – 1500 = 0

x² – 50x + 30x – 1500 = 0

x(x – 50) + 30(x – 50) = 0

(x – 50) (x + 30) = 0

⇒ x = 50 or x = – 30

Rejecting -ve value, because number of children cannot be negative.

∴ x = 50

Hence, the original number of children is 50.

Mean = 24 (given)

∴ (15a+810)/(30+a)= 24

15a + 810 = 720 + 24a

⇒ 24a – 15a = 810 – 720

⇒ 9a = 90

⇒ a = 10

Hence, the value of a is 10.

Steps of Construction :

1. Draw a line segment AB = 6.5 cm.
2. At B, construct an angle of 120° and cut off BC = 5 cm.
3. Join AC, to have ∆ABC.
4. Draw the perpendicular bisectors of line segments AB and BC.
5. Let they intersect each other in 0.
6. With 0 as centre and radius OA or OB or OC, draw the circumcircle of ∆ABC.
7. Produce perpendicular bisector of line segment AB and let it intersect the circumcircle of ∆ABC at D.
8. Join AD and CD.
   Thus, quad. ABCD is the required quadrilateral.

Q.  9 (a) Priyanka has a recurring deposit account of ₹1000 per month at 10% per annum. If she gets ₹5550 as interest at the time of maturity, find the total time for which the account was held. 

(b) In ΔPQR, MN is parallel to QR and  

  (ii) Prove that ΔOMN and ΔORQ are similar. 

  (iii) Find, Area of ΔOMN : Area of ΔORQ 

  (c) The following figure represents a solid consisting of a right circular cylinder with a hemisphere at one end and a cone at the other. Their common radius is 7 cm. The height of the cylinder and cone are each of 4 cm. Find the volume of the solid. 

Answer:

1. Amount deposited per month = ₹ 1000

           Rate of interest = 10% p.a.

            Interest = ₹ 5550

n² + n = 1332

n² + n – 1332 = 0

n² + 37n – 36n – 1332 = 0

n(n + 37) – 36(n + 37) = 0

(n – 36) (n + 37) = 0

n = 36 or n = – 37

Rejecting – ve value of n, we have n = 36

Hence, the total time for which the account was held, was 36 month or 3 years.

(b) Given that:

In ∆PQR, MN is parallel to QR

∴ By using Basic Proportionality theorem, we have

(c) Here, radius of cone = radius of cylinder = radius of hemisphere = 7 cm

Height of cone = 4 cm

Height of cylinder = 4 cm

Q.  10 (a) Use Remainder theorem to factorize the following polynomial: 

              2x³ + 3x² − 9x − 10. 

(b) In the figure given below ‘O’ is the centre of the circle. If QR = OP and ∠ORP = 20^°. 

      Find the value of ‘x’ giving reasons. 

(c) The angle of elevation from a point P of the top of a tower QR, 50m high is 60^o and that of the tower PT from a point Q is 30^o. Find the height of the tower PT, correct to the nearest meter.

Answer :

(a)  Let p(x) = 2x³ + 3x² – 9x – 10

Factors of constant term 10 are ± 1, ± 2, ± 5

Put x = 2, we have

p(2) =2(2)³ + 3(2)² – 9(2) – 10

= 16 + 12 – 18 – 10

= 0

∴ (x – 2) is a factor of p(x)

Put x = – 1, we have

P(-1) =2(-1)³ + 3(-1)² – 9 (-1) – 10

= – 2 + 3 + 9 – 10 = 0

∴ (x + 1) is a factor of p(x)

Thus, (x + 1) (x – 2) i.e.,x2 – x – 2 is a factor of p(x)

Hence, (x + 1), (x – 2) and (2x + 5) are the factors of given polynomial 2x³ + 3x² – 9x – 10.

(b) 

Here, in ∆OPQ

OP = OQ = r

Also, OP = QR [Given]

OP = OQ = QR = r

In ∆OQR, OQ = QR

∠QOR = ∠ORP = 20°

And ∠OQP = ∠QOR + ∠ORQ

= 20° + 20°

= 40°

Again, in ∆ OPQ

∠POQ = 180° – ∠OPQ – ∠OQP

= 180°- 40° – 40°

= 100°

Now, x° + ∠POQ + ∠QOR = 180° [a straight angle]

x° + 100° + 20° = 180°

x° = 180° – 120° = 60°

Hence, the value of x is 60.

(c) 

Here, Height of the tower (QR) = 50 m

Height of the tower (PT) = h m

Inrt. ∠ed ∆ PQR, ∠RPQ = 60°

Also, inrt. ∠ed ∆ QPT, ∠TQP = 30°

Hence, the required height of tower PT is 17 m (nearest to metre). 

   Q.  11 (a) The 4^th term of an A.P. is 22 and 15^th term is 66. Find the first term and the common difference. Hence find the sum of the series to 8 terms. 

(b) Use Graph paper for this Q. . 

    A survey regarding height (in cm) of 60 boys belonging to Class 10 of a school Was conducted. The following data was recorded: 

Height in cm	135 – 140	140 – 145	145 – 150	150 – 155	155 – 160	160 – 165	165 – 170
No. of  boys	4	8	20	14	7	6	1

Taking 2cm = height of 10 cm along one axis and 2 cm = 10 boys along the other  axis draw an ogive of the above distribution. Use the graph to estimate the  following: 

 (i) the median 

 (ii) lower Quartile 

 (iii) if above 158 cm is considered as the tall boys of the class. Find the number of  boys in the class who are tall. 

Answer.

(a) Let a and d be the first term and common difference of the required A.P.

∴ a4 = 22

⇒ a + 3d = 22 ………(i)

And a15 = 66

⇒ a + 14d = 66 ………..(ii)

Subtracting (i) from (ii), we have

(14d – 3d) = 66 – 22

11d = 44

d = 4

From (i), we have

a + 3(4) = 22

a = 22 – 12 = 10

Thus, a = 10 and d = 4

Now, Sn = n/2 [2a + (n – 1)d]

⇒ S8= 8/2[2(10) + (8-1)4]

S8 = 4 [20 + 28]

S8 = 4 x 48 S8 = 192

(b) Given data was recorded as :

Plot the points (140,4), (145,12), (150,32), (155,46), (160,53), (165,59) and (170,60). Join them free hand to get the required ogive.

Now, from the graph, we obtain :

(i) Median height (in cm) = 149.5 cm

(ii) Lower Quartile = 146 cm ‘

(iii) Number of boys who are tall e., height above 158 cm = 60 – 51 = 9.

MATHEMATICS 

SECTION A 

Q.1 (a) Solve the following inequation and write down the solution set: 

11x − 4 < 15x+ 4 ≤ 13x + 14, xєW

Represent the solution on a real number line. 

(b) A man invests ₹4500 in shares of a company which is paying 7.5% dividend.  If ₹100 shares are available at a discount of 10%.

Find: 

     (i) Number of shares he purchases. 

     (ii) His annual income. 

(c) In a class of 40 students, marks obtained by the students in a class test (out of 10) are given below:

Marks	1	2	3	4	5	5	7	8	9	10
Number of Students	1	2	3	3	6	10	5	4	3	3

Calculate the following for the given distribution: 

      (i) Median 

      (ii) Mode 

Q.2 (a) Using the factor theorem, show that (x – 2) is a factor of x³ + x² − 4x− 4. Hence factorise the polynomial completely. 

(b) Prove that:

(cosec θ − sin θ)(sec θ − cos θ)(tan θ + cot θ) = 1 

(c) In an Arithmetic Progression (A.P.) the fourth and sixth terms are 8 and 14 respectively. Find then 

     (i) first term 

     (ii) common difference 

     (iii) sum of the first 20 terms. 

Q.3  (a) Simplify 

(b) M and N are two points on the X axis and Y axis respectively. 

P (3, 2) divides the line segment MN in the ratio 2 : 3.

Find: 

(i) the coordinates of M and N 

(ii) slope of the line MN. 

(c) A solid metallic sphere of radius 6 cm is melted and made into a solid cylinder of height 32 cm. Find the: 

 

      (i) radius of the cylinder 

      (ii) curved surface area of the cylinder ( Take π = 3.14) 

 

Q.4 (a) The following numbers, K + 3, K + 2, 3K – 7 and 2K – 3 are in proportion. Find K.

(b) Solve for x the quadratic equation x² − 4x − 8 = 0. Give your answer correct to three significant figures. 

(c) Use ruler and compass only for answering this question. Draw a circle of radius 4 cm. Mark the center as O. Mark a point P outside the circle  at a distance of 7 cm from the center. Construct two tangents to the circle from the  external point P.Measure and write down the length of any one tangent. 

SECTION B 

Q.5 (a) There are 25 discs numbered 1 to 25. They are put in a closed box and shaken thoroughly. A disc is drawn at random from the box. Find the probability that the number on the disc is: 

      (i) an odd number 

      (ii) divisible by 2 and 3 both. 

      (iii) a number less than 16. 

(b) Rekha opened a recurring deposit account for 20 months. The rate of interest is 9% per annum and Rekha receives  Rs. 441 as interest at the time of maturity.  

Find the amount Rekha deposited each month. 

(c) Use a graph sheet for this question.  Take 1 cm = 1 unit along both x and y axis. 

     (i) Plot the following points: A(0,5), B(3,0), C(1,0) and D(1,–5) 

    (ii) Reflect the points B, C and D on the y axis and name them as B’, C’ and D’ respectively. 

   (iii) Write down the coordinates of B’, C’ and D’. 

   (iv) Join the points A, B, C, D, D’, C’, B’, A in order and give a name to the closed figure ABCDD’C’B’. 

Q.6 (a) In the given figure, ∠PQR = ∠PST = 90^o, PQ = 5 cm and PS = 2 cm. 

     (i) Prove that ΔPQR ~ ΔPST. 

      (ii) Find Area of ΔPQR : Area of quadrilateral SRQT. 

(b) The first and last term of a Geometrical Progression (G.P.) are 3 and 96 respectively. If the common ratio is 2, find: 

     (i) ‘n’ the number of terms of the G.P. 

     (ii) Sum of the n terms. 

(c) A hemispherical and a conical hole is scooped out of a solid wooden cylinder. 

     Find the volume of the remaining solid where the measurements are as follows: 

     The height of the solid cylinder is 7 cm, radius of each of hemisphere, cone and cylinder is 3 cm.

     Height of cone is 3 cm. Give your answer correct to the nearest whole number. Take π = 22/7

Q.7 (a) In the given figure AC is a tangent to the circle with center O.  

      If ∠ADB = 55^o, find x and y. Give reasons for your answers. 

(b) The model of a building is constructed with the scale factor 1 : 30.  

      (i) If the height of the model is 80 cm, find the actual height of the building in  meters.  

     (ii) If the actual volume of a tank at the top of the building is 27 m³, find the volume  of the tank on the top of the                model. 

(c) Given  M  = 6 I, where M is a matrix and I is unit matrix of order 2 x 2. 

     (i) State the order of matrix M. 

    (ii) Find the matrix M. 

Q.8 (a) The sum of the first three terms of an Arithmetic Progression (A.P.) is 42 and the product of the first and third term is 52. Find the first term and the common difference. 

(b) The vertices of a ΔABC are A(3, 8), B(–1, 2) and C(6, –6). Find: 

      (i) Slope of BC. 

      (ii) Equation of a line perpendicular to BC and passing through A. 

(c) Using ruler and a compass only construct a semi-circle with diameter BC = 7cm.  

Locate a point A on the circumference of the semicircle such that A is equidistant from B and C. Complete the cyclic quadrilateral ABCD, such that D is equidistant from AB and BC. Measure ∠ADC and write it down.  

Q.9 (a) The data on the number of patients attending a hospital in a month are given below. Find the average (mean) number of patients attending the hospital in a month by using the shortcut method. Take the assumed mean as 45. Give your answer correct to 2 decimal places.

Number of patients	10 – 20	20 – 30	30 – 40	40 – 50	50 – 60	60 – 70
Number of Days	5	2	7	9	2	5

(b) Using properties of proportion solve for x, given 

(c) Sachin invests ₹ 8500 in 10%, ₹ 100 shares at ₹ 170. He sells the shares when the price of each share rises by ₹ 30. He invests the proceeds in 12% ₹ 100 shares at ₹ 125. Find: 

     (i) the sale proceeds. 

    (ii) the number of ₹ 125 shares he buys. 

    (iii) the change in his annual income. 

Q.10 (a) Use graph paper for this question. The marks obtained by 120 students in an English test are given below: 

Marks	0–10	10–20	20–30	30–40	40–50	50–60	60–70	70–80	80–90	90–100
No. of students	5	9	16	22	26	18	11	6	4	3

Draw the give and hence, estimate: 

     (i) the median marks. 

    (ii) the number of students who did not pass the test if the pass percentage was 50. 

    (iii) the upper quarterly marks. 

(b) A man observes the angle of elevation of the top of the tower to be 45^o. He walks towards it in a horizontal line through its base. On covering 20 m the angle of  elevation changes to 60^o. Find the height of the tower correct to 2 significant figures.

Q.11 (a) Using the Remainder Theorem find the remainders obtained when  x³ + (kx + 8)x + k is divided by x + 1 and x – 2. Hence find k if the sum of the two remainders is 1. 

(b) The product of two consecutive natural numbers which are multiples of 3 is equal to 810. Find the two numbers.  

(c) In the given figure, ABCDE is a pentagon inscribed in a circle such that AC is a diameter and side BC||AE. If ∠BAC = 50°, find giving reasons: 

     (i) ∠ACB 

    (ii) ∠EDC 

    (iii) ∠BEC 

    Hence prove that BE is also a diameter